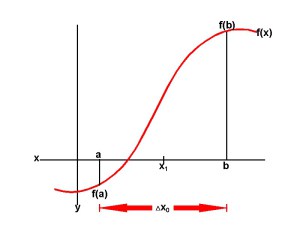
The bisection method is one of the simplest and most reliable of iterative methods for the solution of nonlinear equations. This method, also known as binary chopping or half-interval method, relies on the fact that if f(x) is real and continuous in the interval a < x < b, and f(a) and f(b) are of opposite signs, that is,
f(a)*f(b) < 0
then there is at least one real root in the interval between a and b.
Bisection method is a closed bracket method and requires two initial guesses. It is the simplest method with slow but steady rate of convergence.
Features of Bisection Method:
- Type – closed bracket
- No. of initial guesses – 2
- Convergence – linear
- Rate of convergence – slow but steady
- Accuracy – good
- Programming effort – easy
- Approach – middle point
Bisection Method Algorithm and Flowchart:
Algorithm:
Start
- Decide initial values for x1 and x2 and stopping criterion, E.
- Compute f1 = f(x1) and f2 = f(x2).
- If f1 * f2>0, x1 and x2 do not bracket any root and go to step 7;
Otherwise continue. - Compute x0 = (x1+x2)/2 and compute f0 = f(x0)
- If f1*f0 < 0 then
set x2 = x0
else
set x1 = x0
set f1 = f0 - If absolute value of (x2 – x1)/x2 is less than error E, then
root = (x1 + x2)/2
write the value of root
go to step 7
else
go to step 4 - Stop.
Flow Chart
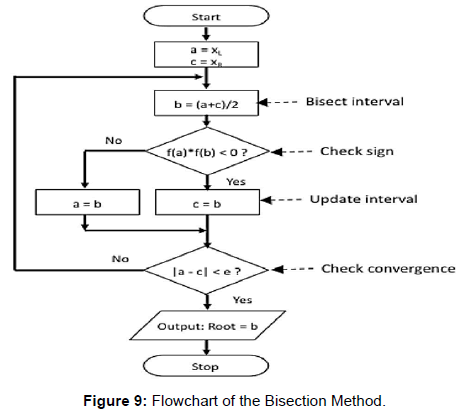
Above given Algorithm and Flowchart of Bisection Methods Root computation is a simple and easier way of understanding how the bracketing system works, algorithm and flowchart may not follow same procedure, yet they give the same outputs.
Tabular Example of Bisection Method Numerical Computation
Consider f(x) = x3 + 3x – 5, where [x1 = 1, x2 = 2] and E = 0.001.
| i | x1 | x0 | x2 | f(x1) | f(x0) | f(x2) |
|---|---|---|---|---|---|---|
| 1 | 1 | 1.5 | 2 | –1 | 2.875 | 9 |
| 2 | 1 | 1.25 | 1.5 | –1 | 0.703125 | 2.875 |
| 3 | 1 | 1.125 | 1.25 | –1 | –0.201171875 | 0.703125 |
| 4 | 1.125 | 1.1875 | 1.25 | –0.201171875 | 0.237060546875 | 0.703125 |
| 5 | 1.125 | 1.15625 | 1.1875 | –0.201171875 | 0.014556884765625 | 0.237060546875 |
| 6 | 1.125 | 1.140625 | 1.15625 | –0.201171875 | –0.0941429138183594 | 0.014556884765625 |
| 7 | 1.140625 | 1.1484375 | 1.15625 | –0.0941429138183594 | –0.0400032997131348 | 0.014556884765625 |
| 8 | 1.1484375 | 1.15234375 | 1.15625 | –0.0400032997131348 | –0.0127759575843811 | 0.014556884765625 |
| 9 | 1.15234375 | 1.154296875 | 1.15625 | –0.0127759575843811 | 0.000877253711223602 | 0.014556884765625 |
Note: Bisection method guarantees the convergence of a function f(x) if it is continuous on the interval [a,b] (denoted by x1 and x2 in the above algorithm. For this, f(a) and f(b) should be of opposite nature i.e. opposite signs. The slow convergence in bisection method is due to the fact that the absolute error is halved at each step. Due to this the method undergoes linear convergence, which is comparatively slower than the Newton-Raphson, secant or false-position method.
Bisection Method – Code in C Programming
Method 1:
This program in C is used to demonstrate bisection method. Bisection method is one of the many root finding methods.
In this method we are given a function f(x) and we approximate 2 roots a and b for the function such that f(a).f(b)<0
Then we find another point
c=(a+b)/2
if f(c)==0
then root=c;
else
if f(a).f(c)<0
b=c;
if f(b).f(c)<0
a=c;
and we repeat these steps for the given number of iterations.
#include"stdio.h"
#include"math.h"
double F(double x)
{
return(pow(x,3)+3*x-5);//This return the value of the function
}
int main()
{
printf("This program illustrates the bisection method in C\n");
printf("x^3 + 3*x - 5 = 0\n");
double x0,x1;
printf("Enter the first approximation to the root\n");
scanf("%lf",&x0);
printf("Enter the second approximation to the root\n");
scanf("%lf",&x1);
int iter;
printf("Enter the number of iterations you want to perform\n");
scanf("%d",&iter);
int ctr=1;
double l1=x0;
double l2=x1;
double r,f1,f2,f3;
//We check if the initail approximations are the root or not
if(F(l1)==0)
r=l1;
else
if(F(l2)==0)
r=l2;
else
{
while(ctr <= iter)
{//this is an implementation of the algorithm mentioned above
f1=F(l1);
r=(l1+l2)/2.0;
f2=F(r);
f3=F(l2);
if(f2==0)
{
r=f2;
break;
}
printf("The root after %d iteration is %lf\n",ctr,r);
if(f1*f2<0)
l2=r;
else
if(f2*f3<0)
l1=r;
ctr++;
}
}
printf("The approximation to the root is %lf",r);
getch();
}
/*A sample run of the program was carried out and the results were found as:-
This program illustrates the bisection method in C
x^3 + 3*x - 5 = 0
Enter the first approximation to the root
1
Enter the second approximation to the root
2
Enter the number of iterations you want to perform
9
The root after 1 iteration is 1.500000
The root after 2 iteration is 1.250000
The root after 3 iteration is 1.125000
The root after 4 iteration is 1.187500
The root after 5 iteration is 1.156250
The root after 6 iteration is 1.146025
The root after 7 iteration is 1.148438
The root after 8 iteration is 1.152344
The root after 9 iteration is 1.154297
The root is 1.154297
*/
Method 2:
Source Code for Bisection Method
for equation f(x) = x^3 – 4*x – 9
#include "math.h"
#include "conio.h"
float fun (float x)
{
return (x*x*x - 4*x - 9);
}
void bisection (float *x, float a, float b, int *itr)
/* this function performs and prints the result of one iteration */
{
*x=(a+b)/2;
++(*itr);
printf("Iteration no. %3d X = %7.5f\n", *itr, *x);
}
void main ()
{
int itr = 0, maxmitr;
float x, a, b, allerr, x1;
printf("\nEnter the values of a, b, allowed error and maximum iterations:\n");
scanf("%f %f %f %d", &a, &b, &allerr, &maxmitr);
bisection (&x, a, b, &itr);
do
{
if (fun(a)*fun(x) < 0)
b=x;
else
a=x;
bisection (&x1, a, b, &itr);
if (fabs(x1-x)<allerr)
{
printf("After %d iterations, root = %6.4f\n", itr, x1);
return 0;
}
x=x1;
}
while (itr<maxmitr);
printf("The solution does not converge or iterations are not sufficient");
return 1;
}
play youtube
play youtube
xvideos
xporn
Phim sex
What Vaccines Do Dogs Need Annually
Wordle Jan 19
What Is Threshold Amount
My Pet Frame
Box Score For World Series
Louisville Women S Basketball Roster
Apple Savings Account Cons
Cso Criminal Search Bc
What Were Kleenex Tissues Originally Used For
Mens All Birds
Is Better Call Saul Over
Waitrose Warwick Way
Usd To Rm
How Much Is A Fitbit
Civil Liabilities Definition
What Is A Fast Internet Download Speedhulk Smash Birthday Cake
Waitrose Warwick Way
Rabies Vector Species
Gonzo Move
What Is The Sherman Act